Yesterday I left the post with 2 GCJ14 Round 2 unsolved problems. Here are the solutions to those problems
Problem C: Don’t Break The Nile: as I said, we can use Maximum flow algorithm to solve this problem, but actually we don’t have to run the full straightforward MaxFlow algorithm. We can apply the idea of Max-flow = Min-cut to solve this problem. A way that we can find the min-cut to the graph is to draw the min-cut curve going from the west to the east side. Consider the following picture (from the sample test):
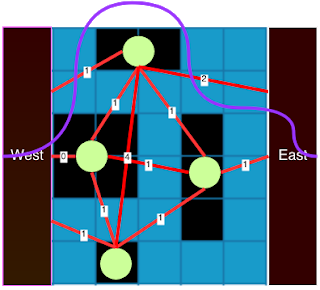
The purple line is a minimum cut on this graph (the network flow graph is not shown). Basically, we try to make a new graph such that all builds are represented as vertices, and there are 2 more vertices for the west and east sides. We added an edge between each pair of vertices (For simplicity, some edges are not shown in the picture). The weight of each edge is the distance between two buildings. In analogy, the cut’s cost between two buildings is the amount of water that can go through the gaps between the buildings. So let’s think a bit of how we can find the minimum cut? ——— Look like a shortest path problem, right? and yes, the cost of the minimum cut is just the shortest path from the west to the east side. That’s it. The size of the entire grid doesn’t matter here. I really like this problem!
About implementation, finding the distance between two buildings are somewhat tricky though. My method is like there are four points on each rectangle. Let’s take the minimum distance between the 16 pairs of points between the two buildings (The distance between two points here is max(abs(p1.x - p2.x), abs(p1.y - p2.y)) - 1). This is not all. We have to consider 4 more cases where two buildings are located side-by-side :)
Now move to the hardest problem: Problem D. Trie Sharding. There are two parts of this problem: 1) Find the maximum total number of nodes of all possible group arrangements. 2) How many group arrangements that results in that maximum number of nodes. To answer the first question, let’s build a trie of all the strings. Consider the following picture for the first sample input (“AAA”, “AAB”, “AB”, “B”):
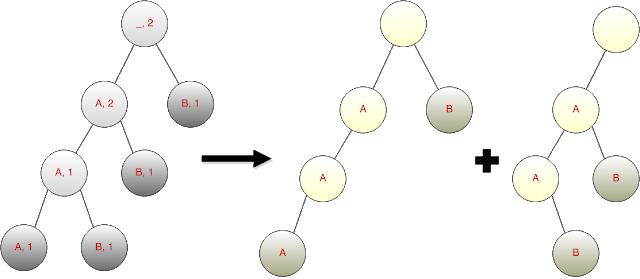
The original trie can be composed of these two tries ({“AAA”, “B”}, {“AAB”, “AB”}). Considering the original trie, the second number on each node indicates how many times this node can appear on different tries (Of course, the number can’t be greater than N). The way that we can calculate all these numbers is to starting from leaves to the root. We can be sure that each node that represents the end of a string can appear only once on a trie, so we can set the second number to 1. For the other nodes, their second number are the sum of the second numbers of all of their children. If the sum is greater than N, set it to N. Finally, the sum of all the second numbers are the total number of the nodes. Answering the second question is harder. In different interpretation, the second number is actually the number of trie subtrees rooted at each node. We claim that that the number of group arrangements is the multiplication of the number of ways to make each subtree. Consider the root subtree as an example. There are 2 subtrees from the first child and 1 subtree from the second child. We have to count the number of ways to combine these 3 subtrees into 2 tries. So the subproblem is that given a list of numbers x (#subtrees on each child), and a number k = min(N, total #subtree), count how many ways we can combine all the subtrees into kk tries (trees). The order doesn’t matter and two subtrees on the same child can’t be in the same resulting subtree.
For example, x = {2, 1}, kk = 2, there are 2 ways: ({X, Y}, {X}) and ({X}, {X, Y}), X is a subtree from the first child and Y is a subtree from the second child. Notice that two x’s need to be in the different trees.
This can be solved by Dynamic Programming:
long long count(vector<int>&x, int kk) {
// dp[i] = the number of ways to combine x into i tries
// C[i][j] = (i choose j)
int sz = x.size();
for (int i = 1; i <= kk; i++) {
dp[i] = 1;
for (int j = 0; j < sz; j++)
// there are i tries, choose x[j] tries for x[j] subtrees
dp[i] = (dp[i] * C[i][x[j]]) % MOD;
for (int j = 1; j < i; j++)
// we subtract dp[i] by the number of ways that we don't use
// all i tries.
dp[i] = (((dp[i] - dp[j] * C[i][j]) % MOD) + MOD) % MOD;
}
return dp[kk];
}
The end!!!